
Vba Exp Function In Excel 5 Examples Exceldemy
The exp(x) from Fortran's EXP() DO !So we need to determine what value (if any) of the constant C 3 makes g(x) = f(x) If we set x=0 and evaluate f(x) and g(x), we get f(x) = cos( 0 ) i sin( 0 ) = 1 g(x) = C 3 e i 0 = C 3 These functions are equal when C 3 = 1 Therefore, cos( x ) i sin( x ) = e i x Justification #2 the series method (This is the usual justification given in textbooks)
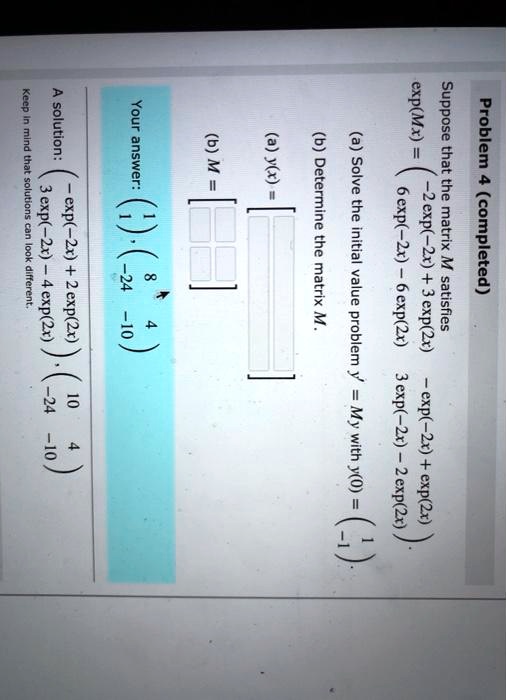
Exp 0 value
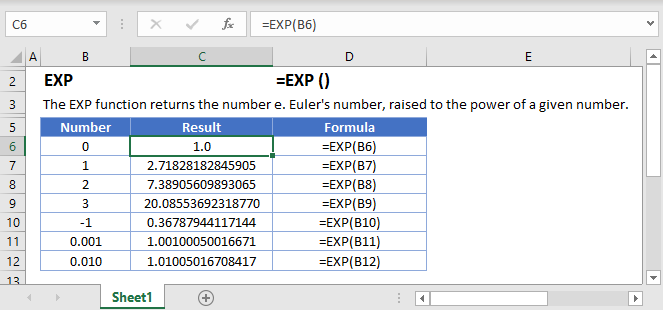
Exp 0 value- 14,950 19 I would suspect both your math teacher and physics teacher are right!If you need to, you can adjust the column widths to see all the data Formula Description Result =EXP (1) Approximate value of e =EXP (2) Base of the natural logarithm e

Experimental Values Of The Variance As A Function Of The Number Of Download Scientific Diagram
Definition and Usage The mathexp() method returns E raised to the power of x (E x) 'E' is the base of the natural system of logarithms (approximately 271) and x is the number passed to it The printed value for MathE is while the value of Mathexp (10), which should be the same value is (one more 5 at the end) From the docs, it sounds like the bits in MathE have been "manually adjusted" to get closer to the actual value of e than the calculation produced by Mathexp (10) The exponent of a number is the constant e raised to the power of the number For example EXP (10) = e^10 = and EXP (10) = e^10 = The exponential of the natural logarithm of a number is the number itself EXP (LOG ( n )) = n And the natural logarithm of the exponential of a number is the number itself LOG
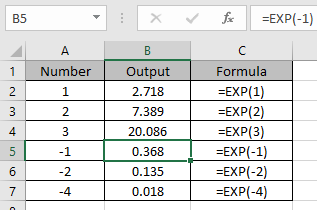
Well, our growth amount is "0x" — after a second, the expandotron obliterates the number and turns it to zero=EXP (value) Here, EXP returns the value of constant e raised to the power of the given value For example, the function =EXP(5) will return the value of e5 Similarly, even if you want to find the value of e raised to a more complex formula, for example, 2x5, you simply need to type =EXP(2x5) This will give the same value as e2x5 Note that y·exp(x)=1·exp(4)=exp(4) as required If we can get x to 0 while maintaining the invariant, then y would be given by y=exp(4)·exp(0)=exp(4)·1=exp(4), and so we will have calculated the desired result in y Suppose we subtract some value k from x Then, to maintain the invariant, the new y value y′ will have to satisfy
Exp 0 valueのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | 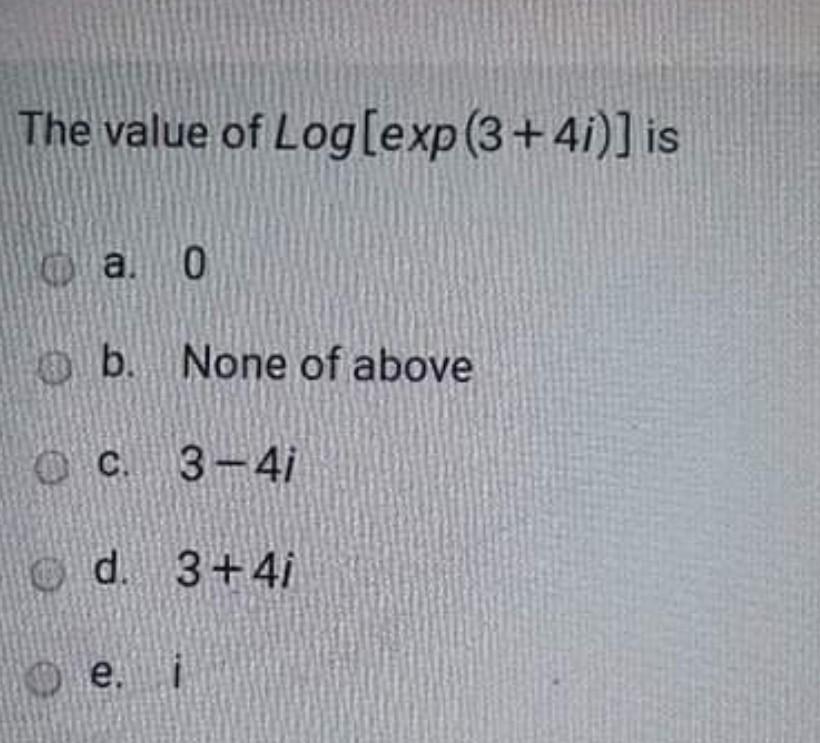 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions | 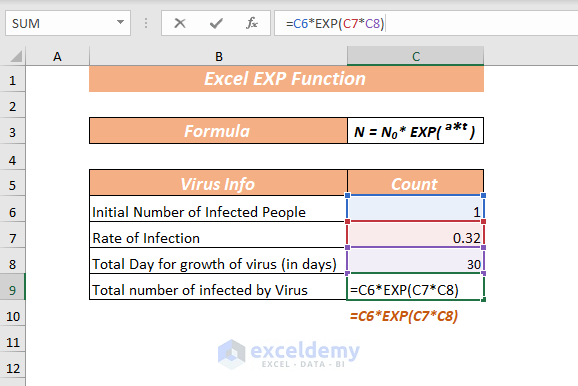 Domain And Range Of Exponential And Logarithmic Functions |
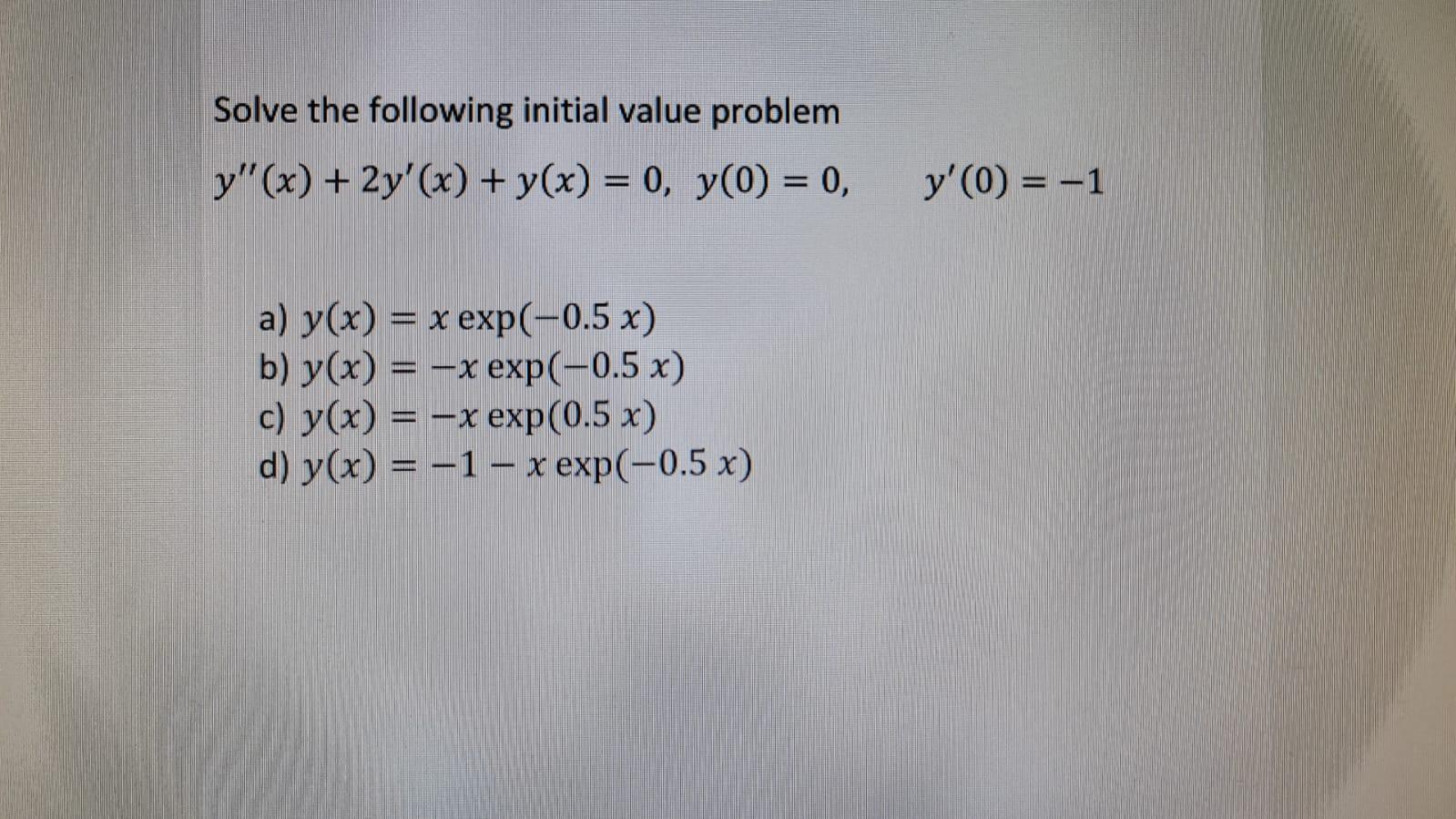 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions | 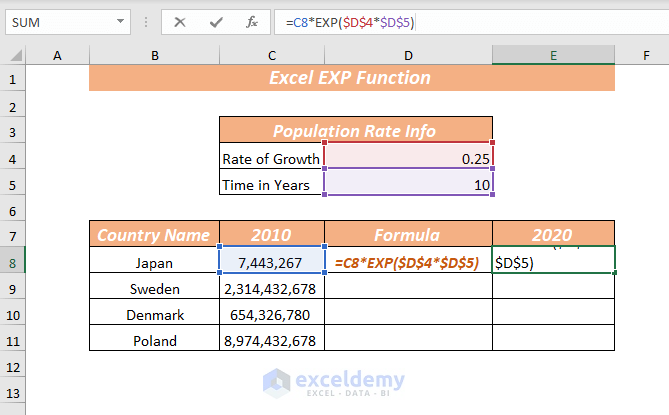 Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
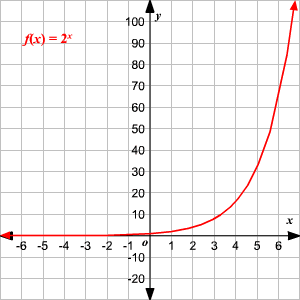 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions | 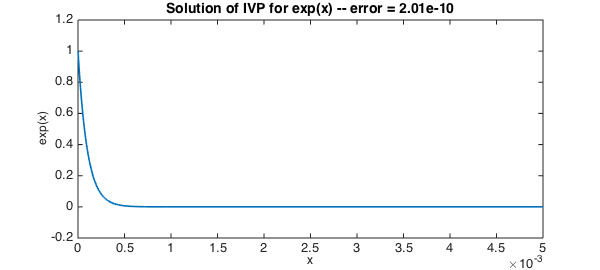 Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
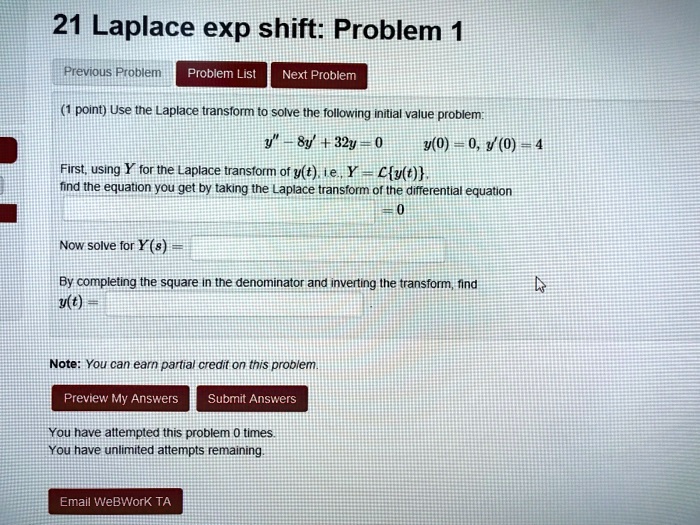
 Domain And Range Of Exponential And Logarithmic Functions | 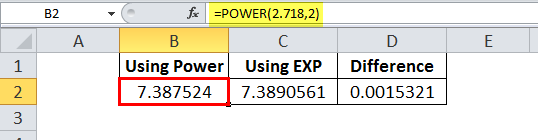 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions | 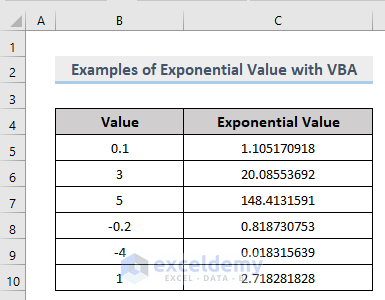 Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | 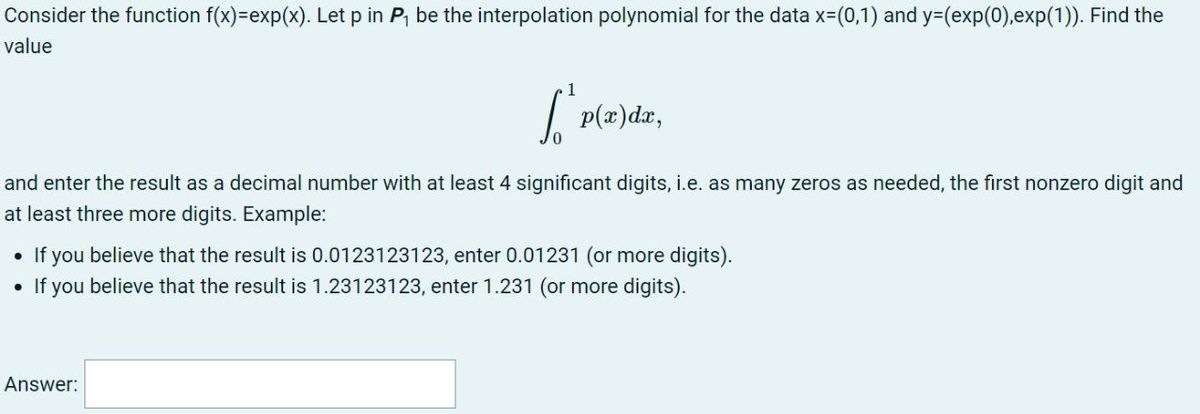 Domain And Range Of Exponential And Logarithmic Functions | 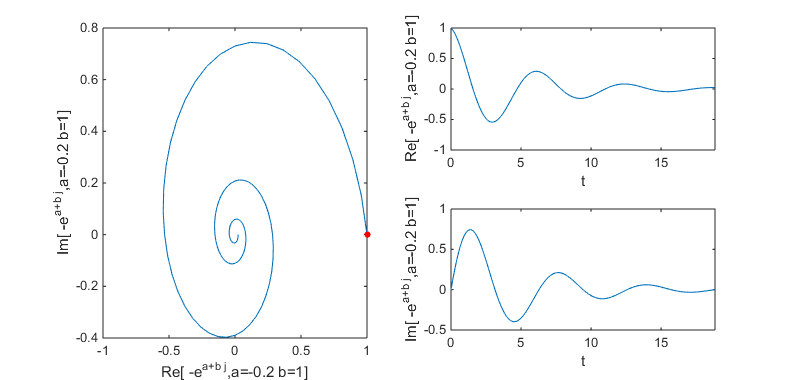 Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | 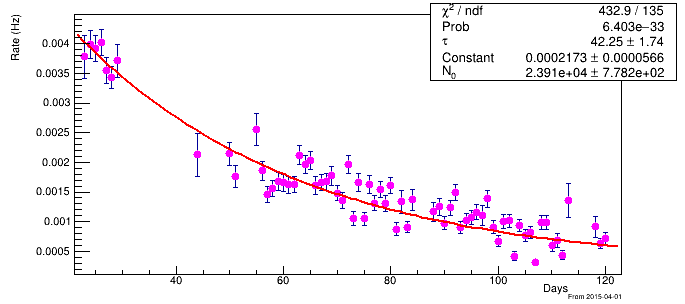 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
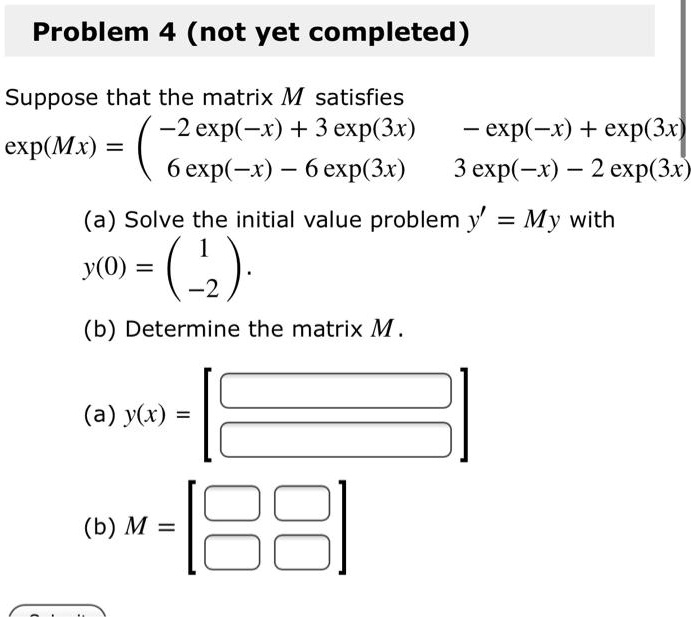 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | 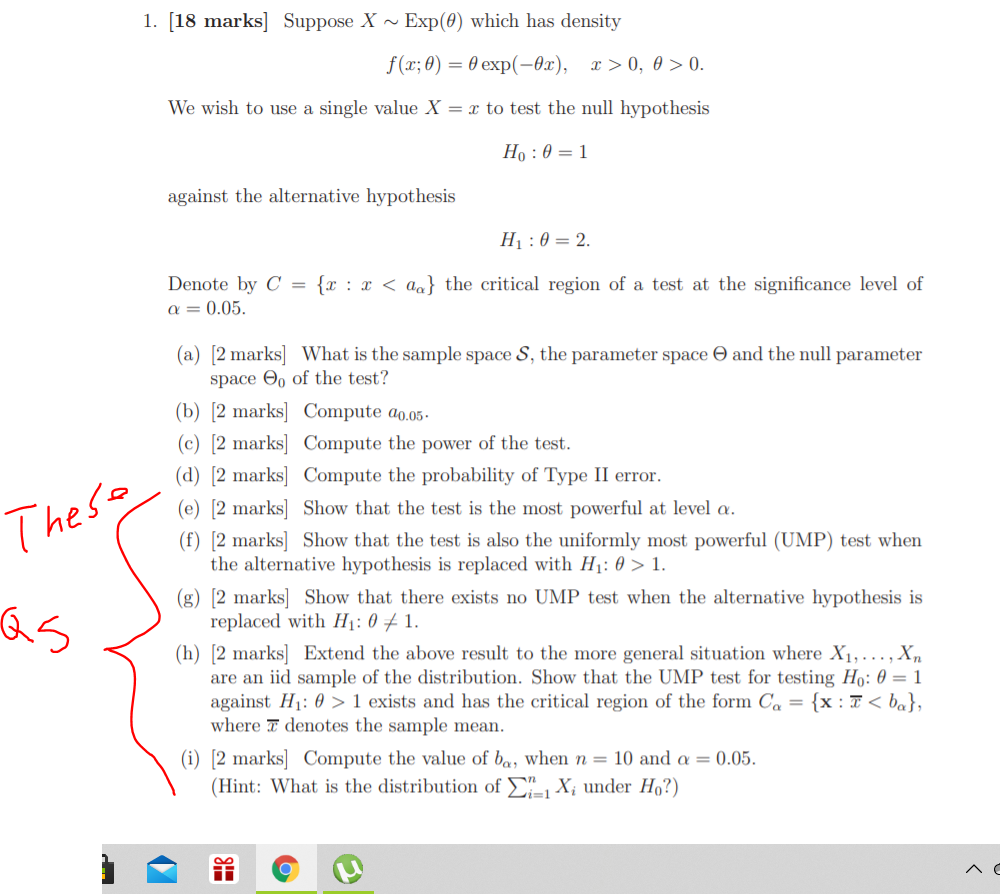 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
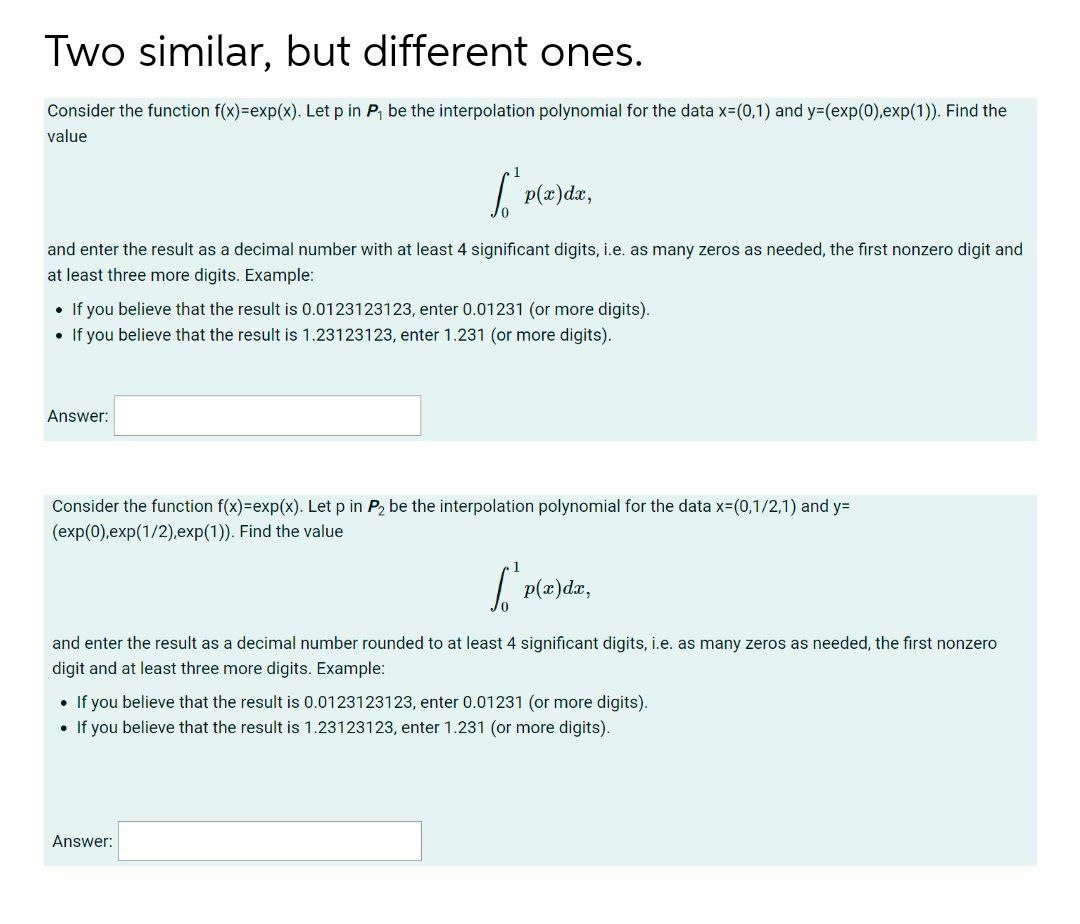 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |
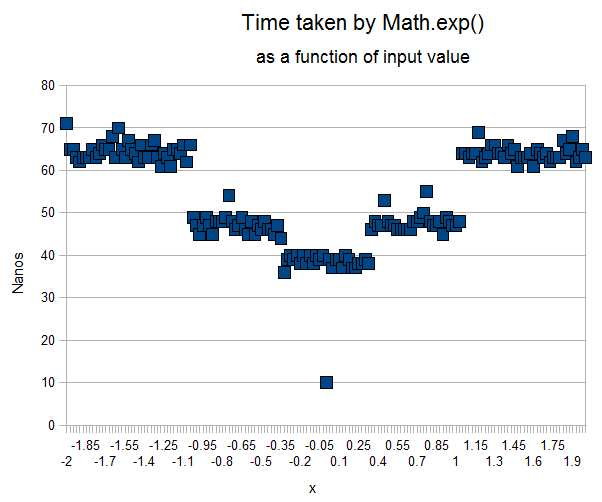 Domain And Range Of Exponential And Logarithmic Functions | Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions | 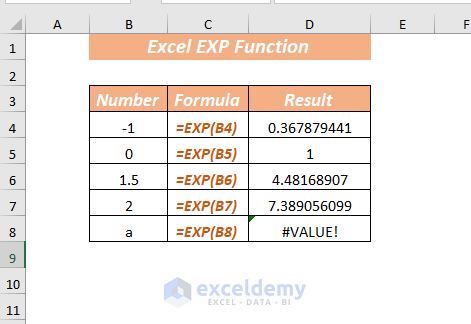 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
 Domain And Range Of Exponential And Logarithmic Functions |  Domain And Range Of Exponential And Logarithmic Functions |
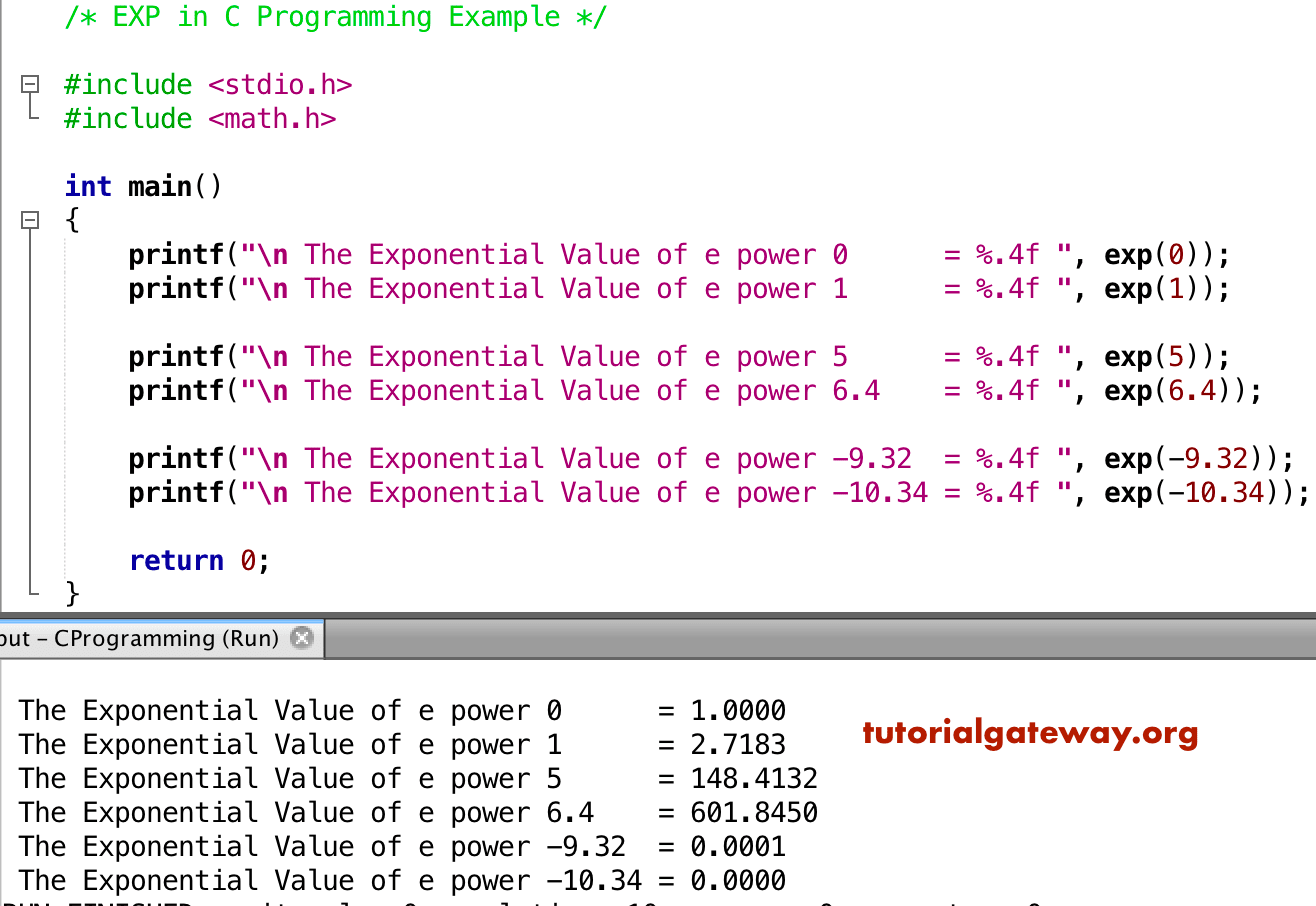
The exp () function in C returns the exponential ( Euler's number) e (or 2718) raised to the given argument The function can take any value ie, positive, negative or zero in its parameter and returns result in int, double or float or long double The exp () function returns the value in the range of 0, infThe exp () function returns the value in the range of 0, ∞ If the magnitude of the result is too large to be represented by a value of the return type, the function returns HUGE_VAL with the proper sign, and an overflow range error occurs
Incoming Term: exp 0 value,




0 件のコメント:
コメントを投稿